Next: Average bipartite entanglement Up: SILQCS - Simple Interpretive Previous: Visibility
RDO(bit labels);outputs the reduced density operator of the qubits specified by bit labels. To show each vector in the output of the reduced density operator in the format of binary digits, you may command
RDOb(bit labels);
Similarly,
RDOsave (bit labels, file name);outputs the reduced density operator of the qubits specified by bit labels to the file of file name. Further analysis with the saved matrix should be performed in another calculator such as Octave. This is possible when a user converts it to the matrix in another format (See Sec. 5.1).
Note: These three commands does not change the current state
in calculation. They only show or save a reduced density operator.
In general, a reduced density operator of specified qubits (
![]() )
is given by
)
is given by
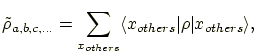 |
(9) |
Let the component system ![]() comprise the specified qubits
comprise the specified qubits
![]() ,
and the component system
,
and the component system ![]() comprise the other qubits. Then the reduced
density operator of
comprise the other qubits. Then the reduced
density operator of ![]() is defined as
is defined as
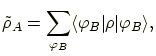 |
(10) |