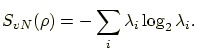Generally, the von Neumann entropy of a density matrix 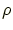 is defined by
is defined by
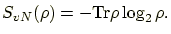 |
(14) |
We use the binary logarithm (base 2) in this software.
It is also written by using the eigenvalues
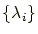 of
of 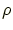 as
as
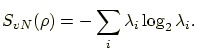 |
(15) |
This is because a density matrix 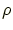 can be diagonalized by a proper
unitary transformation. Such a transformation preserves eigenvalues of
can be diagonalized by a proper
unitary transformation. Such a transformation preserves eigenvalues of
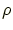 . A density matrix
. A density matrix 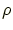 is an Hermitian matrix and its
eigenvalues are non-negative real numbers.
is an Hermitian matrix and its
eigenvalues are non-negative real numbers.
The command
SvN;
shows the von Neumann entropy of the current density matrix.
The command
SvNRDO(bit labels);
shows the von Neumann entropy of the reduced density operator of the
qubits specified by bit labels.
root
2004-11-07